Listar por palabra clave "Rotación"
RiuNet: Repositorio Institucional de la Universidad Politécnica de Valencia
- RiuNet repositorio UPV
- :
- Listar por palabra clave
JavaScript is disabled for your browser. Some features of this site may not work without it.
Buscar en RiuNet
Listar
Mi cuenta
Ayuda RiuNet
Admin. UPV
Listar por palabra clave "Rotación"
Mostrando ítems 1-13 de 13
-
Cerdá Boluda, Joaquín (Universitat Politècnica de València, 2019-05-13)En este polimedia se expone la forma de animar objetos como un todo, mediante la animación de transformaciones afines
-
Armesto Ángel, Leopoldo (Universitat Politècnica de València, 2020-06-05)Este vídeo explica las operaciones de traslación y rotación en el software de simulación de robots CoppeliaSim
-
Izquierdo Sebastián, Joaquín (Universitat Politècnica de València, 2016-07-06)En este objeto resolvemos las denominadas ecuaciones de Euler del cuerpo rígido sin forzamiento externo. Las tres variables independientes y1, y2 e y3, son las coordenadas del vector de rotación, mientras que las variables ...
-
Fayos Sancho, Juan (Universitat Politècnica de València, 2008-05-07)
-
Ramón Sánchez, Ramón (Universitat Politècnica de València, 2019-06-11)[ES] El presente Trabajo Final de Grado trata sobre el cálculo y la ejecución de muros pantalla. Recoge las comprobaciones, de acuerdo con el CTE (Código Técnico de la Edificación), así como detalla el proceso constructivo ...
-
Rubio Sánchez, Antonio (Universitat Politècnica de València, 2023-10-17)[ES] El objetivo del presente proyecto es el diseño y dimensionado de una red de riego por goteo de una explotación de hortícolas de 5,8 ha, situada en el término municipal de Valencia en el entorno de la huerta de ...
-
Morata Lázaro, María Carmen (Universitat Politècnica de València, 2022-09-02)[ES] Con este trabajo se pretende mostrar la problemática existente con la rotación de personal de administración y servicio en la administración pública y su conexión con la puesta en valor de la fuga de talento humano. ...
-
Gomis Hilario, Oscar (Universitat Politècnica de València, 2008-04-14)Definición y significado físico del momento de inercia de un sistema discreto y continuo. Ejemplos.
-
Portero López, Violeta Yolanda (Universitat Politècnica de València, 2020-05-19)[ES] Optimización del cálculo mediante la comparación de diferentes metodologías y fórmulas, definición de parámetros óptimos para la recopilación de datos durante el registro del movimiento para minimizar el error en el ...
-
Gómez De Barreda Ferraz, Diego (Universitat Politècnica de València, 2016-06-20)En este video se indica la rotación típica en una zona muy concreta de la huerta litoral de la provincia de Valencia. Se dan 3 cultivos, dos de ellos con gran valor comercial debido a la época tan temprana de cosecha y el ...
-
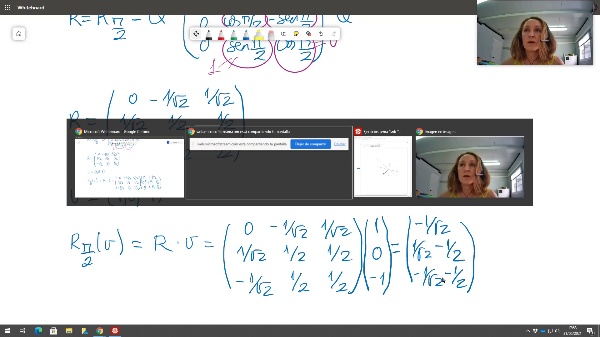
Pérez Peñalver, María José (2021-06-09)Con este video podrás girar vectores en el espacio respecto de un eje cualquiera que pase por el origen. Para ello utilizarás la llamada matriz de rotación, el intrumento matemático que permite girar objetos en el espacio ...
-
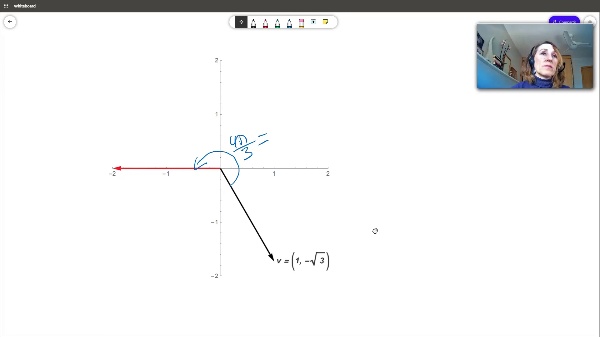
Pérez Peñalver, María José (2021-03-25)Este objeto de aprendizaje construye la matriz de rotación en el plano y la aplica a la rotación de vectores. También repasa algunas de sus propiedades.
-
Cordón Fernández, Fernando (Universitat Politècnica de València, 2011-02-07)Transformación espacial con Processing
Mostrando ítems 1-13 de 13

Universitat Politècnica de València. Unidad de Documentación Científica de la Biblioteca (+34) 96 387 70 85 · RiuNet@bib.upv.es